1. 트리(Tree)
트리는 정점(Node)와 선분(Branch)을 이용하여 사이클이 이루어지지 않게 구성된 자료구조이다.
트리의 특징
- 트리는 계층 모델이다.
- 트리는 비순환 그래프이다.
- 노드가 N개인 트리는 항상 N-1개의 간선을 가진다.
- 순회는 Pre-order, In-order, Post-order로 이루어진다.
- 트리는 이진트리, 이진 탐색 트리, 균형 트리, 이진 힙 등이 있다.
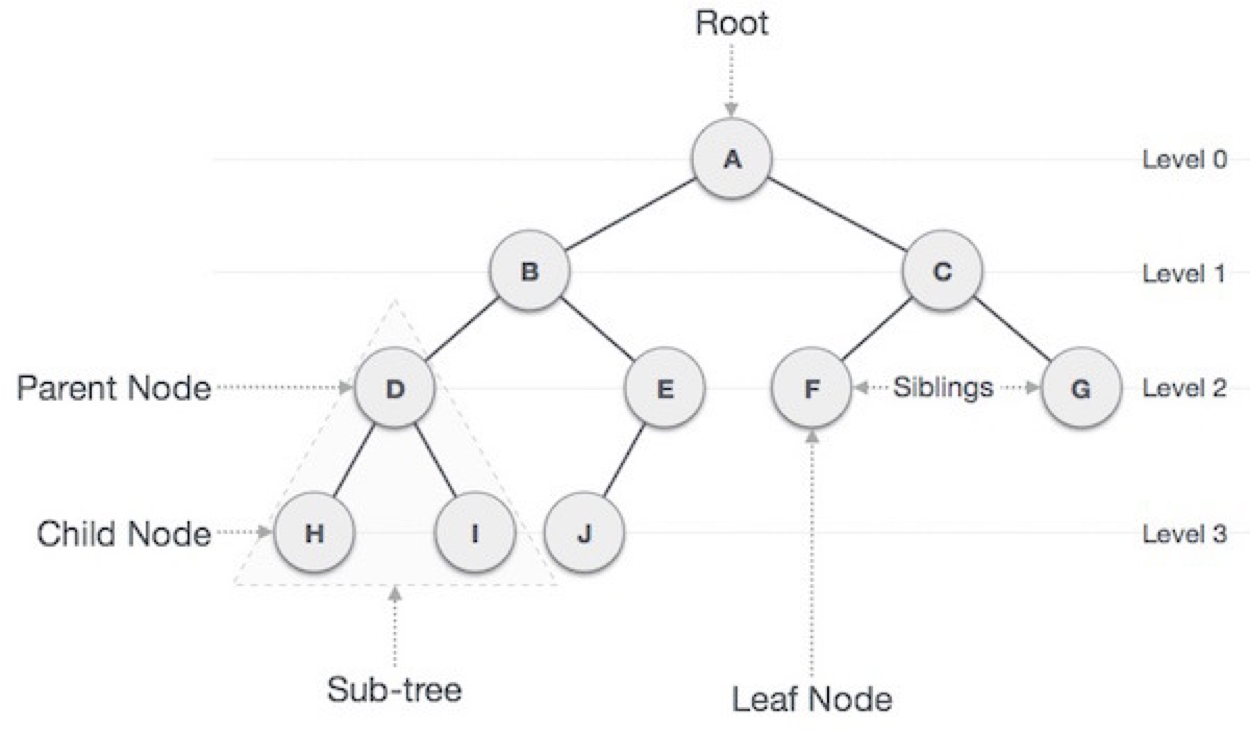
트리의 용어
- 루트 노드(root node) : 부모가 없는 노드, 트리는 하나의 루트 노드 만을 가진다.
- 단말 노드(leaf node) : 자식이 없는 노드
- 내부(internal) 노드 : 단말 노드가 아닌 노드
- 간선(edge) : 노드를 연결하는 선
- 형제(sibling) : 같은 부모를 가지는 노드
- 조상 노드(ancestors node) : 임의의 노드에서 루트 노드에 이르는 경로상에 있는 노드들 (D의 조상은 B, A이다)
- 노드의 크기(size) : 자신을 포함한 모든 자손 노드의 개수
- 노드의 깊이(depth) : 루트에서 어떤 노드에 도달하기 위해 커쳐야하는 간선 수
- 노드의 레벨(level) : 트리의 특정 깊이를 가지는 노드의 집합
- 노드의 차수(degree) : 각 노드에서 뻗어나온 가지의 수 (D의 차수는 2이다.)
- 트리의 차수(degree of tree) : 트리에서 가장 큰 차수
- 트리의 높이(height) : 가장 깊숙히 있는 노드의 깊이 (3)
2. 그래프(Graph)
노드와 노드를 연결하는 간선들로 구성된 자료구조
그래프의 특징
- 그래프틑 네트워크 모델이다.
- 노드들 사이에 방향/무방향 경로를 가질 수 있다.
- 그래프틑 순환 혹은 비순환이다.
- 그래프틑 크게 방향 그래프와 무방향 그래프가있다.
그래프의 용어
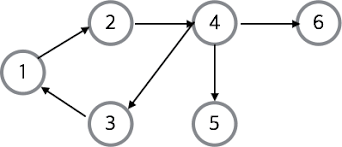
- 정점(vertext) : 위치라는 개념
- 간선(edge) : 정점을 연결하는 선
- 인접 정점(adjacent vertex) : 간선에 직접 연결된 정점
- 차수(degree) : 한 정점에 연결된 간선의 수 (주로 무방향 그래프에서 사용)
- 입력 차수(in-degree) : 한 정점으로 들어오는 간선의 수 (주로 방향그래프에서 사용)
- 출력 차수(out-degree) : 한 정점에서 나가는 간선의 수(주로 방향그래프에서 사용)
- 사이클(cycle) : 한 정점에서 출발하여 시작했던 정점으로 돌아오는 경로
- 가중치 그래프 : 간선마다 가중치 값이 매겨져있는 그래프
그래프의 종류
무방향 그래프(Undirected Graph)
- 간선을 통해 양방향으로 갈 수 있다.
- 정점 A와 정점 B를 연결하는 간선은 (A,B), (B,A) 이다.
방향 그래프(Directed Graph)
- 간선에 방향성이 존재하는 그래프
- A -> B로 갈 수 있는 간선은 (A, B)로 표시한다.
가중치 그래프(Weighted Graph)
- 간선을 이동하는데 비용이나 가중치가 할당된 그래프
- 네트워크라고도 한다.
참조 : https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html
https://justicehui.github.io/easy-algorithm/2018/03/19/GraphIntro/
'IT > 자료구조 & 알고리즘' 카테고리의 다른 글
| [자료구조] JAVA - Queue 구현 소스 (0) | 2020.11.12 |
|---|---|
| [알고리즘] 퀵 정렬 (0) | 2020.03.08 |
| [자료구조] 배열, 연결리스트, 스택, 큐 (0) | 2020.03.04 |
| [Java] 쉘 정렬 (Shell Sort) (0) | 2019.12.06 |
| [Java] 버블 정렬 (Bubble Sort) (0) | 2019.12.06 |